ENSO(El Niño-Southern Oscillation)对全球气候及人类社会有着深远影响。与ENSO暖事件(El Niño)和冷事件(La Niña)相关的洪水、干旱、热浪和其他极端事件对许多国家的农业生产、粮食安全、淡水资源、公共卫生、发电和经济活力等有着重大的影响。ENSO还会扰乱海洋和陆地生态系统、远洋渔业和全球碳循环的正常运作。
人们对ENSO的理解和预报能力在过去几十年中不断提高。与此同时,气候系统本身也在不断演变。自18世纪中叶工业革命开始以来,人类活动通过化石燃料和砍伐森林,将大气中温室气体的浓度提高到前所未有的水平,导致地球不断变暖。这在全球和区域地表气温的上升、冰川融化、北极海冰消失、海洋热含量增加、海平面上升、极端天气事件增多以及其他很多系统性环境变化指标,如栖息地丧失和物种灭绝中都有体现。这些对当前社会的深远影响在未来可能会更加明显。在此背景下,气候变化是否已经改变了、或者将来是否会改变ENSO的特征及其影响方式,是当前地球系统科学在处理一些最紧迫的问题时需要予以回答的基础问题。
由于其年际振荡特征,ENSO的机理和建模研究大多从年际异常场的角度开展。为此,气候平均态被视为恒定的外部输入,只有在其之上演变的异常场才是被关注的核心,如各种概念模型或盒子模型、简单模型和中等复杂程度模型等。这些模型通过将热带太平洋的海气耦合过程围绕气候平均态进行线性化的方式来简化问题。这一简单而有效的处理方式使它们备受欢迎,并在 ENSO 相关研究中一直发挥着主导作用。
然而,由于这类模型的平均态是外部提供的,这使得平均态决定着异常场的反馈强度,而年际异常场对平均态的调制过程则被完全忽略了。事实上,近年来的许多研究都强调了后者的重要性。为了更加全面地研究ENSO的年际异常变化以及它们与气候平均态之间潜在的相互作用,从全场的角度构建模型势在必行,因为它可以同时对两者进行模拟。因此,这类模型可以对异常模型无法回答的问题提供潜在解决方案,例如,极端El Niño的年代际爆发性特征、ENSO与太平洋年代际振荡(PDO)之间的关系、全球变暖对ENSO的影响等。
为此,复旦大学大气与海洋科学系副教授方向辉和国际著名非线性动力学专家、荷兰科学院院士Henk Dijkstra教授及其团队成员Claudia Wieners副教授、Francesco Guardamagna构建了一个能够刻画ENSO多样性的全场非线性理论模型(图1)。该模型主要特点包括:
1)可以同时刻画赤道西、中、东太平洋海表温度变化;
2)具有丰富的动力学表现,即随着主要参数的增强,模型会先后出现稳定(衰减)模、简谐振荡模(极限环)、强度调制(Amplitude-Modulated;AM)振荡模;随着参数的进一步增强,模型将进入另一个简谐振荡模和稳定模(图2;图3);
3)可以对El Niño的爆发性出现(即极端El Niño往往每15-20年出现一次,期间则是较弱的ENSO事件;图3e和f)给出非线性解释,即极端El Niño现象可由ENSO极限环模态与不稳定的辐射-对流平衡态通过所谓的同宿(homoclinic)和异宿(heteroclinic)连接而产生;
4)在AM振荡模中,系统出现多周期性和混沌性特征,这些都与观测中的ENSO特征更加符合(如图3c和d);
5)在AM振荡模中,可以出现与观测一致的不对称性特征,即东太海温(TE)变率大于中太海温(TC),且TE(TC)的偏度为正(负)的现象;
6)随着参数的变化,系统不仅能够刻画ENSO属性的变化,而且能够得到气候平均态的相应变化(图4);因此,可以更全面地描述年际和年代际尺度上的非线性相互作用现象;
7)有研究表明,随着气候变暖,平均温跃层深度(H)将减小、辐射-对流平衡态海表温度(Tr)将增大。该模型指出,在这两个参数的变化下,ENSO将首先继续处于AM振荡模区域,随后进入非常狭小的简谐振荡模区域,最后将变为永恒的稳定模(图5)。
为此,该模型可为进一步研究ENSO自身属性、与年代际变化之间的非线性关系,以及对气候变化的响应提供理论工具。
该工作发表在Journal of Climate上:
Fang, X.*, Dijkstra, H., Wieners, C., and Guardamagna F. (2024) A nonlinear full-field conceptual model for ENSO diversity. Journal of Climate. Doi: https://doi.org/10.1175/JCLI-D-23-0382.1.

图1. 全场非线性ENSO理论模型。

图2. 模型对参数ϵ-ζ的动力学特征分布图。区域I为稳定模,区域II为简谐振荡模,区域III为AM振荡模,即系统出现多周期性和混沌性特征。HB和PD曲线分别代表Hopf分叉和倍周期分岔的边界线。另外,在区域III中,深红部分代表“观测”,即在该区域TE变率大于TC,且TE(TC)的偏度为正(负)。

图3. 不同参数(图2中三个红点)下模型自由积分的60年结果。左侧为全场值,右侧为异常值。从上到下的子图中TE的标准差(偏度)分别为1.75 oC (-0.22),1.72 oC (0.35)和1.54 oC (1.36)。而TC的为1.55 oC (-0.55),1.44 oC (-0.20)和1.20 oC (0.36)。其中图c和d的参数位于AM区域,其时间序列表现出了强烈的倍周期与混沌特征。
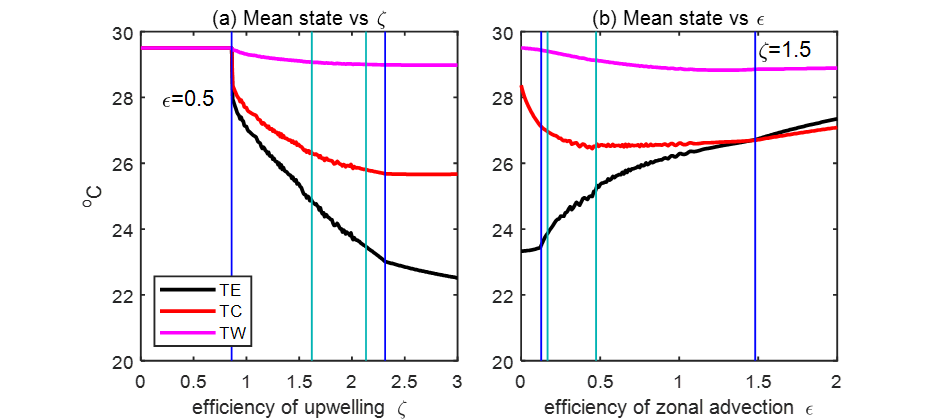
图4. 不同参数下,西、中、东太平洋气候平均态海表温度的变化。由图可见,随着海洋垂向过程的增强,三个区域的海温均逐渐减小,但幅度由西向东逐渐增强,意味着西暖东冷的相对分布,即PDO的负位相;而纬向平流过程的增强作用则恰恰相反,即产生PDO的正位相。
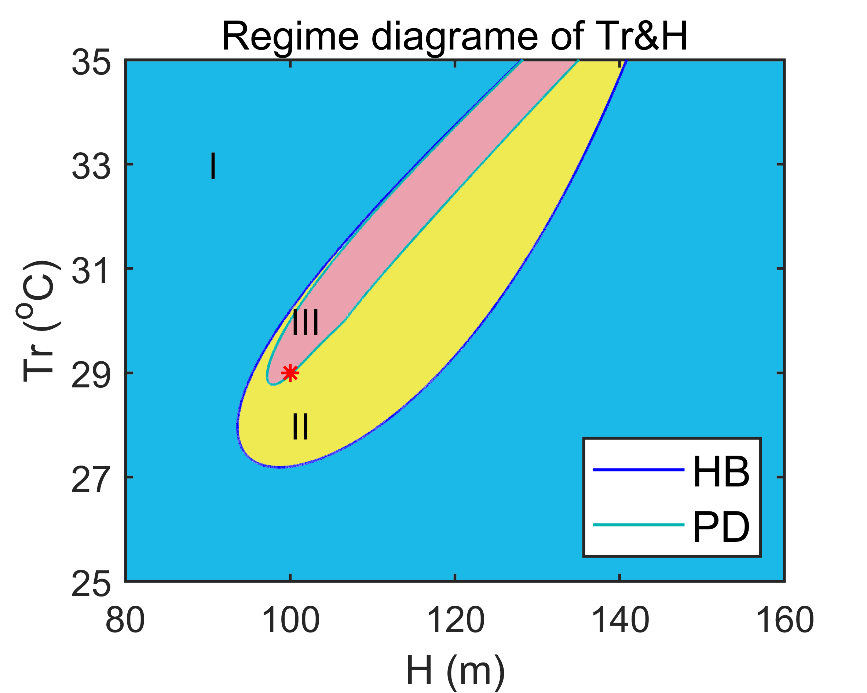
图5.模型对参数Tr(辐射-对流平衡态海温)和H(平均温跃层深度)的动力学特征分布图。其中红色星号为研究中的标准参数(即29 °C和100 m)。由图可见,全球变暖引起的Tr增大和H减小会使系统向左上方移动。